Polyphonyって何だろう(4)使用例:CORDIC with @pure & unroll
Python で書いた関数を Verilog HDL に変換する高位合成コンパイラである Polyphony を使ってみたいと思います。
今回はコンパイル時に python の計算値を埋め込むための @pure デコレーターと、コンパイルの最適化指示の unroll を使用した CORDIC を高位合成してみたいと思います。
Polyphony を使う上での注意点と期待
前回も記載しましたが、polyphony を使用する上で引っ掛かりそうな点を再度書いておきます。
- コメントに日本語を使わない ( utf-8 だとエラーになるようだ)
- y = 2 ** x とかは NG
- pure を使うには env.py の enable_pure = False を True に書き換える必要がある。
- 標準以外のライブラリーを import するとエラーになる ( numpy 等が使えない)
- Testbench で モジュールの戻り値を取得しないとシミュレーションができない。 NG: cordic(y,x) NG -> OK: r = cordic(y,x) ; print(r)
@pure デコレーターを使うと、コンパイル時にその関数を exec で実行して、結果を埋め込んでくれますが、@pure を付けた関数内でも使用できるライブラリーに制限があるようです。numpy は import しただけでエラーになるようです。math は使えるので最低限の関数は使えますが、できれば何でも使えるようになると便利だのですが。
@pure はコンパイル時に python を実行するだけなので、アルゴリズムのデバッグのために、結果を処理するのには使えません。python でのアルゴリズムデバッグを考えると、単純にコンパイル時には読み飛ばしてくれるような表記方法があると便利だと思います。たとえば、現状は、print文での出力もformat処理して書き出せないので、コンパイル時にはコメントアウトする必要がありますが、無視するような指示ができれば、コメントアウトの必要がなくなります。また、結果を matplotlib でグラフ表示して確認したりもできるでしょう。今後に期待したいです。
CORDIC とは
CORDIC は、COordinate Rotation DIgital Computer の略で、反復的なシフト加算演算だけで、正弦関数、余弦関数、逆正弦関数の計算をする方法です。
下記東海大学遠藤研究室の「サルでも分かるCORDICアルゴリズム」が分かりやすいと思います。
http://teamcoil.sp.u-tokai.ac.jp/calculators/column/100224/index.html
ここでは、固定小数点でサイン、コサイン、アークタンジェントの計算を記述します。
Python コード (cordic.py) と簡単な説明
@pure がついている関数は、コンパイル時に実行されて結果のみが組み込まれます。CORDICで使用するテーブルを計算する部分、アルゴリズムの確認用に0度から90度まで5度置きの角度データとその正弦、余弦の固定小数点データを testbench 用に作成する関数を定義するのに使用しています。CORDICの反復計算部分で unroll 指示で最適化しています。
import math import polyphony from polyphony import module, pure, is_worker_running, rule, unroll from polyphony import testbench from polyphony.io import Port from polyphony.typing import bit, bit9, bit24, int32 from polyphony.timing import clksleep, clkfence, wait_value, wait_rising MAXINDEX = 14 FIXBIT = 20 TESTNUM = 19 @pure def power(x): r = pow(2,x) return r @pure def float2bit(x): r = int(x*FIXMUL + 0.5) return r @pure def bit2float(x): r = x / FIXMUL return r @pure def mktable(): theta = [0] * MAXINDEX for i in range(MAXINDEX): r = float2bit(math.degrees(math.atan(1/(2**i)))) theta[i] = r return theta @pure def mkst(): r = 1 for i in range(MAXINDEX): r = r * (math.sqrt(1+1/(2**i)**2)) s = int(1/r*FIXMUL+0.5) return s @pure def mksin(x): r = int(math.sin(math.radians(x))*FIXMUL+0.5) return r @pure def mkcos(x): r = int(math.cos(math.radians(x))*FIXMUL+0.5) return r @pure def mktdata(): tdata = [0] * TESTNUM for i in range(TESTNUM): d = i * 5 tdata[i] = float2bit(d) return tdata @pure def mksdata(): s = [0] * TESTNUM for i in range(TESTNUM): d = i * 5 s[i] = float2bit(math.sin(math.radians(d))) return s @pure def mkcdata(): c = [0] * TESTNUM for i in range(TESTNUM): d = i * 5 c[i] = float2bit(math.cos(math.radians(d))) return c FIXMUL = power(FIXBIT) ST = mkst() THETA = mktable() TDATA = mktdata() SDATA = mksdata() CDATA = mkcdata() # %% Module def cordic_atan(c,s): angle = 0 for i in unroll(range(MAXINDEX)): if ( s < 0): c_next = c - (s >> i) s_next = s + (c >> i) angle += THETA[i] else: c_next = c + (s >> i) s_next = s - (c >> i) angle -= THETA[i] c = c_next s = s_next return -angle def cordic_cs(x): c = ST s = 0 angle = 0 for i in unroll(range(MAXINDEX)): if (x >= angle): c_next = c - (s >> i) s_next = s + (c >> i) angle += THETA[i] else: c_next = c + (s >> i) s_next = s - (c >> i) angle -= THETA[i] c = c_next s = s_next return(c,s) def cordic_sin(x): c,s = cordic_cs(x) return(s) def cordic_cos(x): c,s = cordic_cs(x) return(c) # %% @testbench def cordic_test(): #atancheck print('sin') for i in range(TESTNUM): s = cordic_sin(TDATA[i]) print(SDATA[i],s) # print((i * 5),bit2float(s)) print('cos') for i in range(TESTNUM): c = cordic_cos(TDATA[i]) print(CDATA[i],c) # print((i * 5),bit2float(c)) print('atan') for i in range(TESTNUM): t = cordic_atan(CDATA[i],SDATA[i]) print(TDATA[i],t) # print((i * 5),bit2float(t)) clksleep(10) # %% cordic_test()
実行結果
Python でそのまま実行すると 下記のような出力が得られます。
python関数で計算した時の値とCORDICで計算した時の値を出力しています。CORDIC は反復計算で真値に収束させていく手法なので、打切り誤差が生じているのが分かると思います。
sin 0 80 91389 91455 182083 182013 271391 271315 358634 358653 443147 443039 524288 524385 601438 601530 674012 674080 741455 741489 803256 803199 858943 858880 908093 908039 950333 950382 985339 985330 1012847 1012868 1032646 1032659 1044586 1044580 1048576 1048577 cos 1048576 1048577 1044586 1044580 1032646 1032659 1012847 1012868 985339 985330 950333 950382 908093 908039 858943 858880 803256 803199 741455 741422 674012 674080 601438 601530 524288 524385 443147 443039 358634 358653 271391 271315 182083 182013 91389 91455 0 80 atan 0 4444 5242880 5246580 10485760 10481586 15728640 15724072 20971520 20972414 26214400 26207544 31457280 31463654 36700160 36706710 41943040 41948152 47185920 47188686 52428800 52423688 57671680 57665130 62914560 62908186 68157440 68164296 73400320 73399426 78643200 78647768 83886080 83890254 89128960 89125260 94371840 94367396
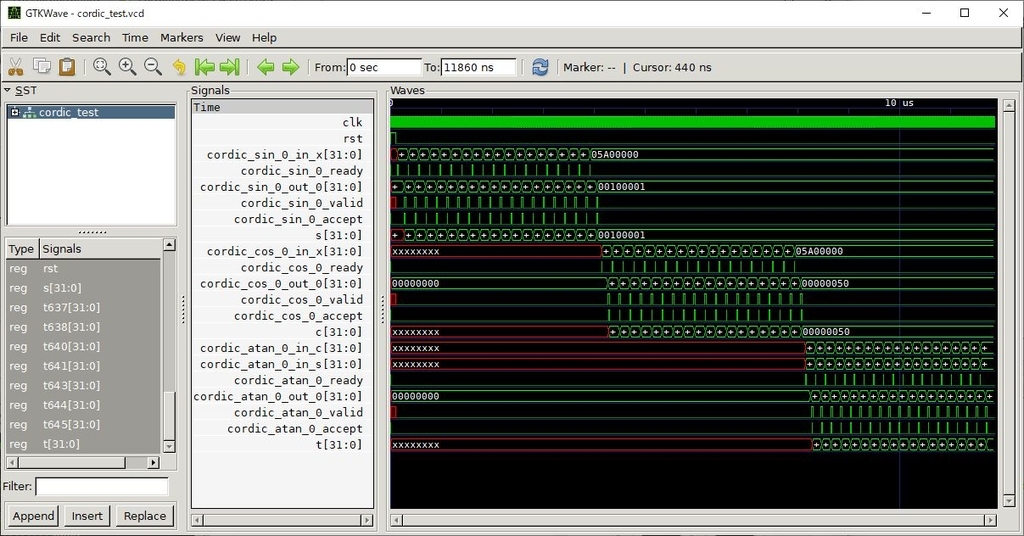
polyphony でコンパイルしてシミュレーションした時の結果が下記になります。unroll で結構速く動いています。